フリーキックの距離の求め方
試合のテレビ放送で、フリーキックがゴールまで何mという距離表示をご覧になると思います。
そこまで正確ではなくおよそですが、三平方の定理を用いてフリーキックの距離の見当をつける方法です。
広告
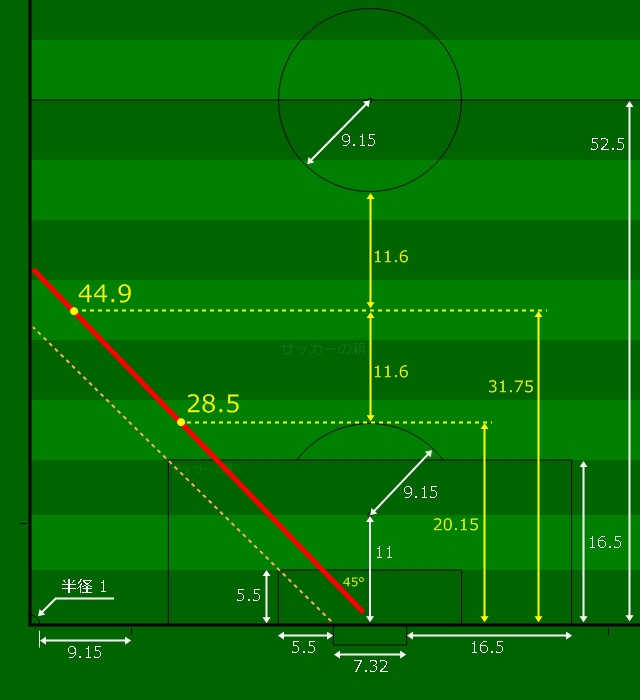
ゴール真正面から45°の場合
45°- 45°の直角三角形
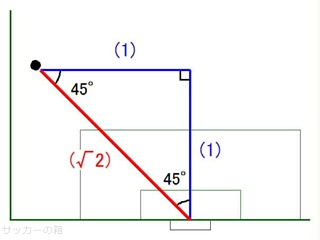
45°- 45°- 90°の直角三角形の辺の長さの比は、1:1:√2です。
赤い(√2)の長さは(1)の、√2 / 1 ≒ 1.41倍です。
よって正面の場合の垂直距離に√2 (1.41)を掛ければフリーキックの距離となります。
実際フィールドでは
（クリック／タップすると拡大し、再度行うと戻ります。）
ニアのゴールポスト→ゴールエリアの角→ペナルティエリアの角を結ぶ直線（図の斜め破線）は完全に45°になることがルール上定められています。
これをゴール幅の半分7.32 / 2 = 3.66mずらせばゴール中央へと向かいます（図の赤線）。
真正面の距離は図の通りで、フリーキックの距離（赤線）も先程の直角三角形を用いて求められます。
- ペナルティアークの高さの場合は、28.5m。
- ペナルティアークとセンターサークルの中間の場合は、44.9m。
ペナルティアークの高さの場合
- ペナルティアークの頂点
- 斜めの距離＝フリーキックの距離
- 11 + 9.15 = 20.15m。
- 20.15 × √2（1.41）≒ 28.5m。
ペナルティアークとセンターサークルの中間の場合
- タッチラインの長さ
- ゴールラインからハーフウェーラインまで
- ペナルティアークとセンターサークルの間
- その中間点
- ゴールラインから中間点まで
- 斜めの距離＝フリーキックの距離
- 105m。
- 105 / 2 = 52.5m。
- 52.5 - 11 - 9.15 - 9.15 = 23.2m。
- 23.2 / 2 = 11.6m。
- 11 + 9.15 + 11.6 = 31.75m。
- 31.75 × √2（1.41）≒ 44.9m。
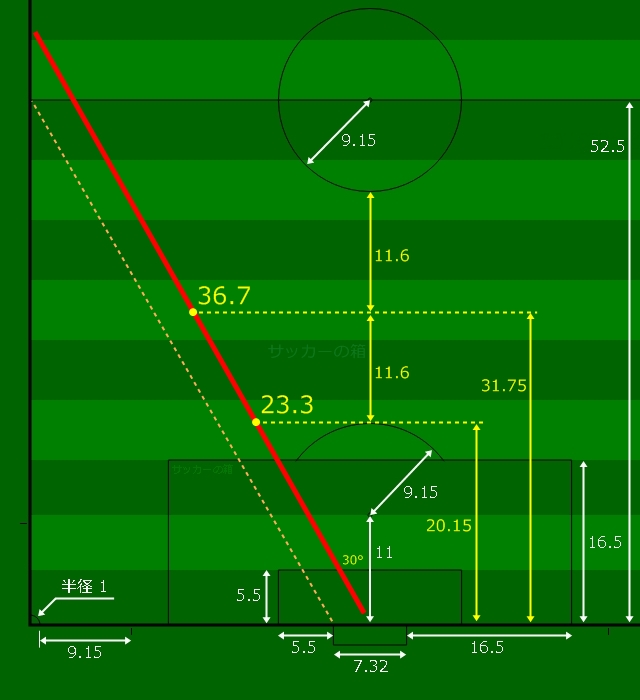
ゴール真正面から30°の場合
30°- 60°の直角三角形
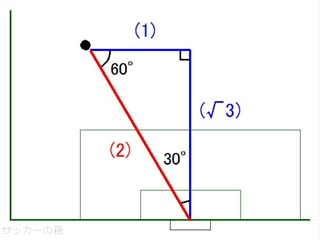
30°- 60°- 90°の直角三角形の辺の長さの比は、√3:1:2です。
赤い(2)の長さは(√3)の、2 / √3 ≒ 1.15倍です。
実際フィールドでは
（クリック／タップすると拡大し、再度行うと戻ります。）
ニアのゴールポストと、タッチラインとハーフウェーラインの交点、を結ぶ直線（図の斜め破線）がだいたい30°です。
フリーキックの距離（赤線）は先程の直角三角形を用いて求められます。
- ペナルティアークの高さの場合は、23.3m。
- ペナルティアークとセンターサークルの中間の場合は、36.7m。
ペナルティアークの高さの場合
- ペナルティアークの頂点
- 斜めの距離＝フリーキックの距離
- 11 + 9.15 = 20.15m。
- 20.15 × 2 / √3 (1.15) ≒ 23.3m。
ペナルティアークとセンターサークルの中間の場合
- ゴールラインから中間点まで
- 斜めの距離＝フリーキックの距離
- 11 + 9.15 + 11.6 = 31.75m。
- 31.75 × 2 √3 (1.15) ≒ 36.7m。
3等分した場合
下図はペナルティアークとセンターサークル間を3等分した場合です。その1区間は23.2 / 3 ≒ 7.73mです。
ペナルティエリアの延長線の場合
斜めの辺は短い辺の2倍なので、このようにも求められます。
- ペナルティエリアの半分の幅
- 斜めの距離＝フリーキックの距離
- 7.32 / 2 + 16.5 = 20.16m。
- 20.16 × 2 ≒ 40.3m。
補足
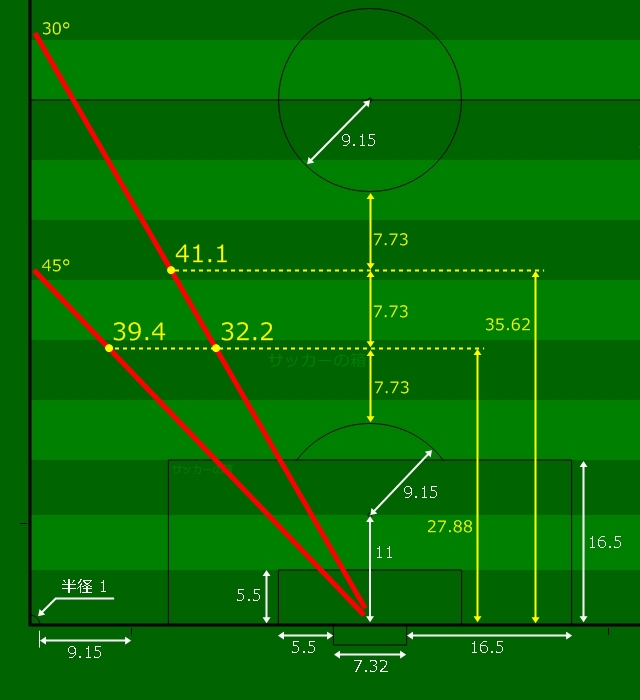
芝目を用いて求める
真正面の距離を、芝目の数を参考にして、今までの計算方法で求めることもできます。
ただしスタジアムによっての違いや、部分的に幅が異なる場合がありますのでその点を考慮しましょう。
上図のようにゴールラインから等分であればいいのですが、ペナルティアーク部分で半端な幅調整をしている場合は多く見ます。
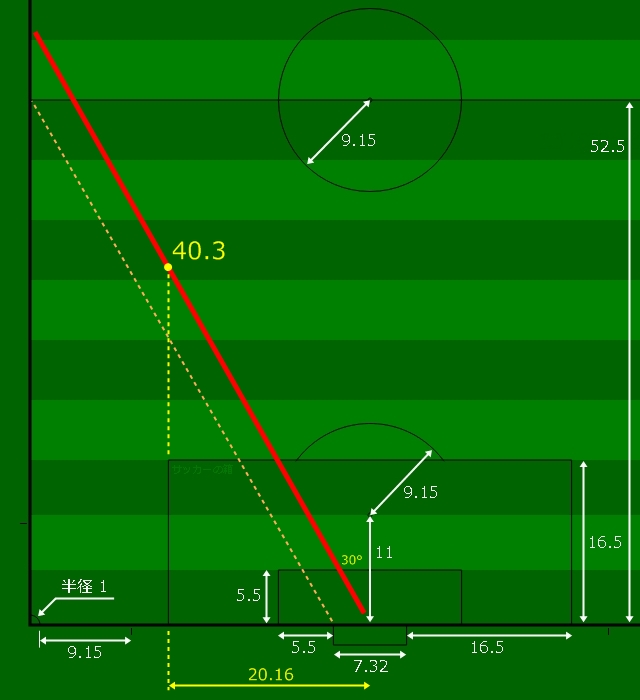
円弧で求める
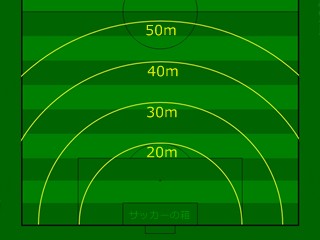
頭の中でのイメージになりますが。
プレーする選手
以上全てゴール中央が基準ですので、蹴る選手からするとこれら計算された値をポストやターゲットの選手などにずらすことになります。
各ラインの名称は下記当サイト関連記事のをご覧願います。
広告
初版